Paso 1 Separa las variables moviendo todos los términos y a un lado de la ecuación y todos los términos x al otro lado: Multiplica ambos lados por dx: dy = ky dx. Divide ambos lados por y: dy y = k dx. Paso 2 Integra ambos lados de la ecuación por separado: Coloca los signos de integración: ∫ dy y = ∫ k dx.. A continuación, se presenta una guía paso a paso para resolver ecuaciones diferenciales por variables separables: 1. Identificar si la ecuación es diferencial y si se pueden separar las variables. Para ello, se debe verificar si la ecuación se puede reescribir de manera que todas las variables independientes estén en un lado y las.

(x^2+4)y'=xy RESOLVER la ecuación DIFERENCIAL por SEPARACIÓN de VARIABLES YouTube
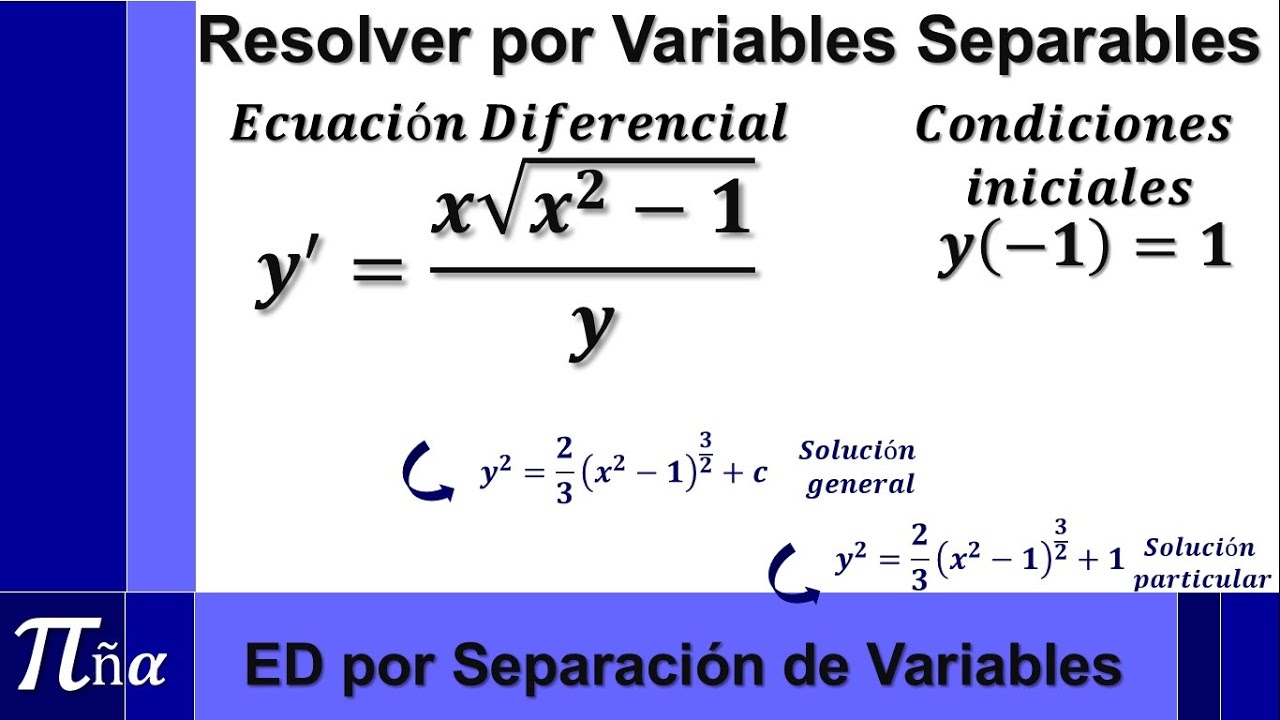
Ecuaciones Diferenciales con condiciones inciales por Separación de Variables (ejemplo 5/5

Problemas Resueltos de Ecuaciones Diferenciales Por Separación De Variables PROBLEMA 1 YouTube

Separación de variables ecuaciones diferenciales(4y + yx^2) dy (2x + xy^2) dx = 0

Ecuaciones Diferenciales por Variables Separables Ejercicio 79 QuedateEnCasa y Aprende
Cálculo21 Ecuaciones diferenciales. Separación de variables.

SEPARACIÓN DE VARIABLES ECUACIONES DIFERENCIALES (Ejemplo 2) Profe Chuy YouTube
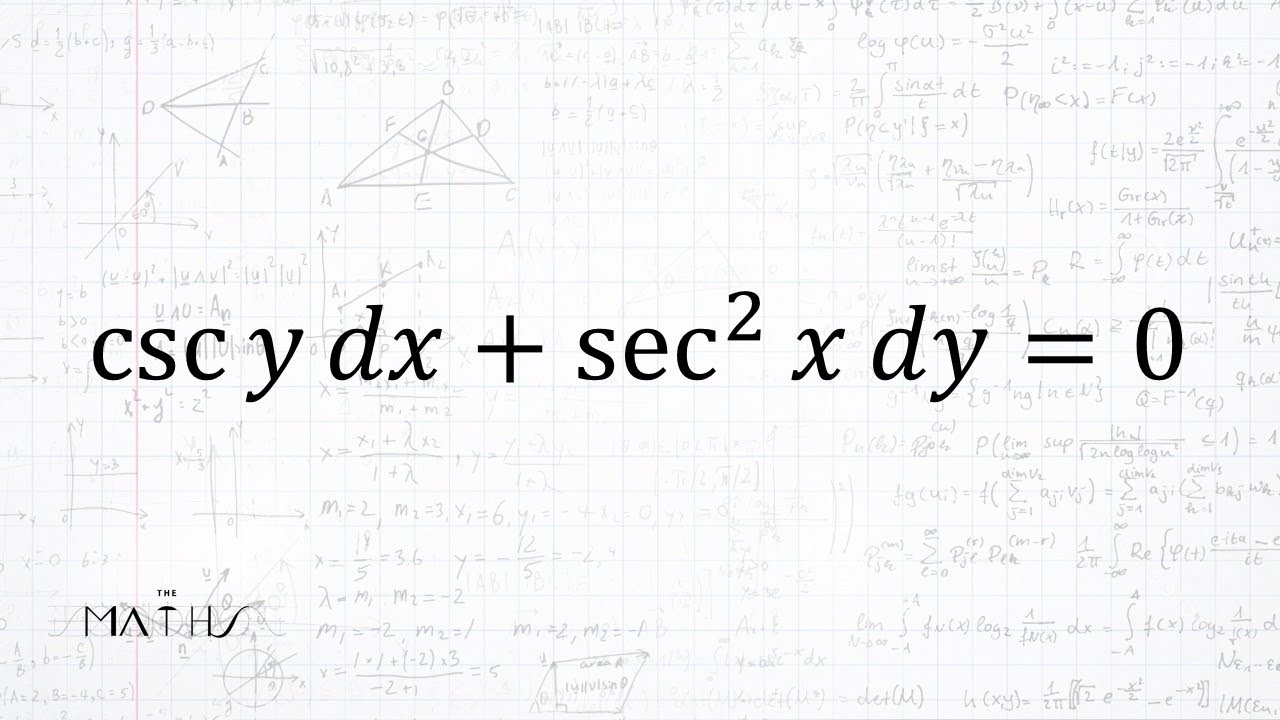
Separación de VARIABLES Ecuaciones Diferenciales YouTube

Ecuaciones diferenciales ordinarias (separación de variables) con comprobación ejemplo 13

Ecuaciones Diferenciales por Separación de Variables (ejemplo 3/5) YouTube

Ecuaciones diferenciales de primer orden de variables separables YouTube

Ecuaciones diferenciales de variables separables Ejemplo 1 YouTube

Ecuaciones Diferenciales Separacion de Variables PDF Ecuaciones diferenciales Ecuaciones

ECUACIONES DIFERENCIALES POR SEPARACIÓN DE VARIABLES EJEMPLO 5 YouTube
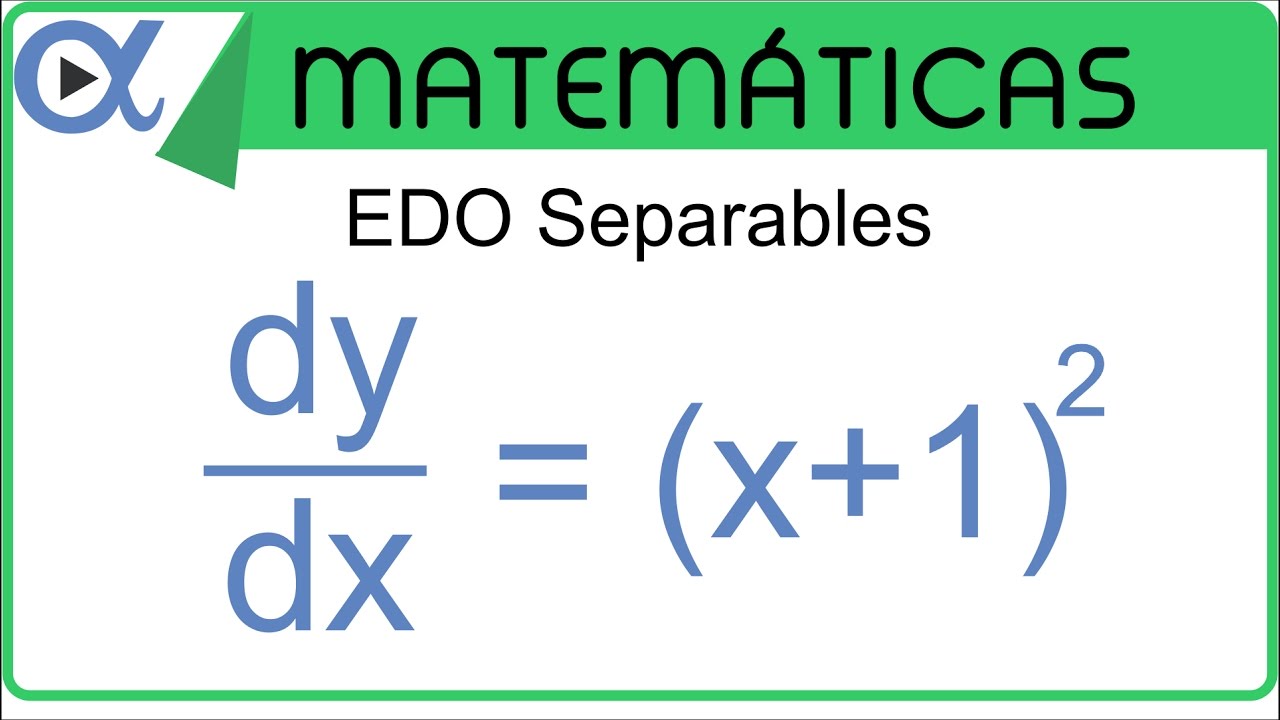
Ecuaciones diferenciales ordinarias (separación de variables) ejemplo 2 Vitual YouTube

02 Ecuaciones diferenciales. Variables Separables. 2da Parte. YouTube
Cálculo21 Ecuaciones diferenciales. Separación de variables.

Ecuaciones diferenciales ordinarias, método de separación de variable. YouTube

Separación de variables ecuaciones diferenciales SoluciónEJERCICIO 8 YouTube

Ecuaciones Diferenciales Separación de Variables 1 YouTube
Contestar. La estrategia del Ejemplo 7.4.1 puede aplicarse a cualquier ecuación diferencial de la forma dy dt = g(y) ⋅ h(t), d y d t = g ( y) ⋅ h ( t), y se dice que cualquier ecuación diferencial de esta forma es separable. Trabajamos para resolver una ecuación diferencial separable mediante la escritura. 1 g(y) dy dt = h(t), 1 g ( y) d.. Una ecuación diferencial separable es cualquier ecuación que se puede escribir en la forma. y ′ = f(x)g(y). El término 'separable' se refiere al hecho de que el lado derecho de la Ecuación\ ref {sep} se puede separar en una función de x veces una función de y. Los ejemplos de ecuaciones diferenciales separables incluyen.