Entonces, el logaritmo natural de un número es la potencia a la cual debe ser elevado el número e para lograr conseguir el valor de tal número. Por ejemplo, tenemos el número 20.08553692318766774092216 y su logaritmo es 3 porque e 3 = 20.08553692318766774092216. Y también se puede decir que el logaritmo de e es 1 porque e 1 = e.. Un número trascendental es un número que no es la raíz de ninguna función polinómica racional. Los ejemplos incluyen e y π. This page titled 3.4.2: Logaritmos comunes y naturales is shared under a CK-12 license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of.

Propiedades de los logaritmos Logaritmo de una potencia Logaritmo de una raíz Cambio de

Análisis de la función logaritmo natural YouTube

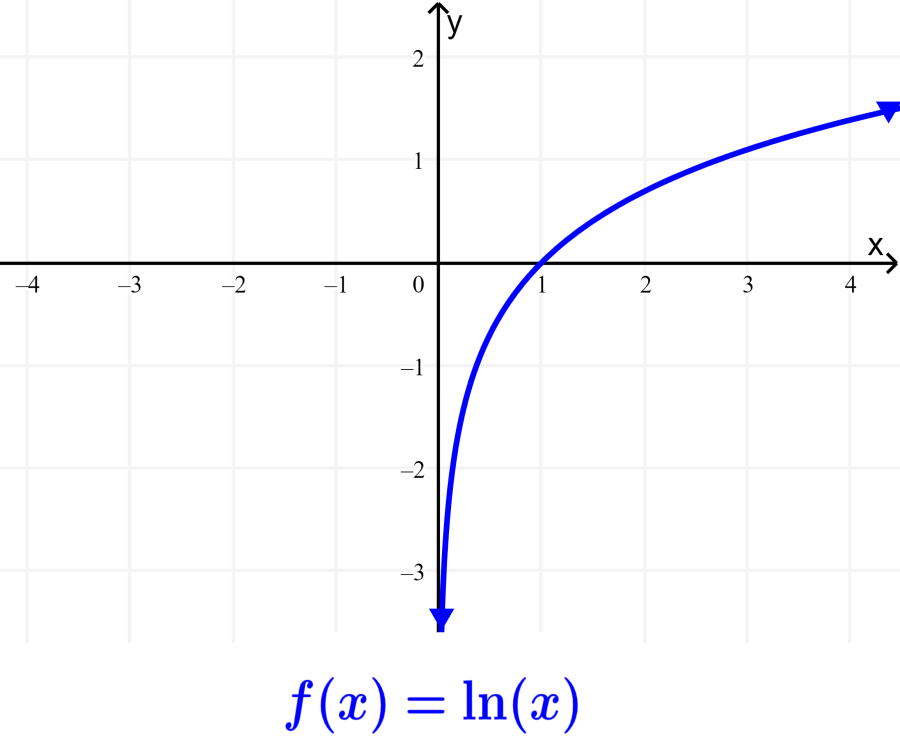
Cual Es La Base De Los Logaritmos Naturales rowrich

Propiedades de los Logaritmos Wiki Número

Partes del Logaritmo.

Matemática Logaritmo natural YouTube

Propiedades de los logaritmos naturales Cursos Online Web

Logaritmo Natural de un Número Complejo (3 ejemplos) YouTube

Logaritmos Introducción conceptos básicos YouTube

Propiedades de los logaritmos YouTube

Logaritmo base 10 y logaritmo natural YouTube

PROPIEDADES DE LOGARITMOS EJEMPLOS Y EJERCICIOS RESUELTOS

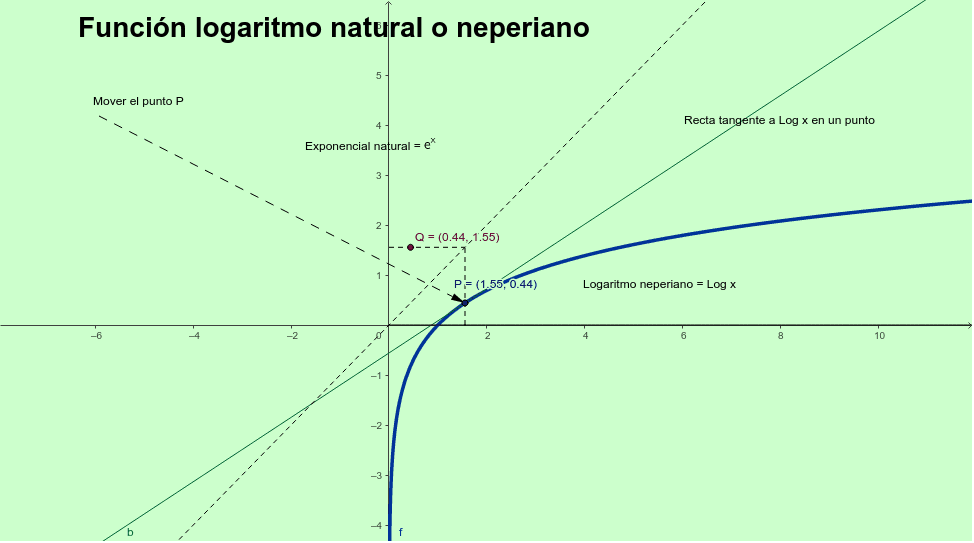
Función logaritmo natural GeoGebra

PROPIEDADES DE LOGARITMOS NATURALES (logaritmo natural de una fracción, multiplicación y

Derivada de Logaritmo Natural Ejemplo 1 YouTube

Regla del logaritmo natural Ejemplos Cálculo Diferencial YouTube

Despejes de funciones con logaritmos

Demostración de la derivada de la función Logaritmo Natural YouTube

Integral por partes para logaritmo natural YouTube

Explicando logaritmos con números naturales YouTube

APOYA ESTE CONTENIDO COMPRANDO EN MI TIENDA NERD: https://www.geekpipro.com COMPRAR POR DEPÓSITO O TRANSFERENCIA (WhatsApp): https://wa.me/message/YG5L34E.. Los logaritmos naturales o logaritmos neperianos son los que tienen base e. Se representan por ln (x) o L (x). Los logaritmos neperianios deben su nombre a su descubridor John Neper y fueron los primeros en ser utilizados. El logaritmo neperiano de x (ln x) es la potencia a la que se debe elevar e para obtener x. ln 1 = 0 e0 = 1.