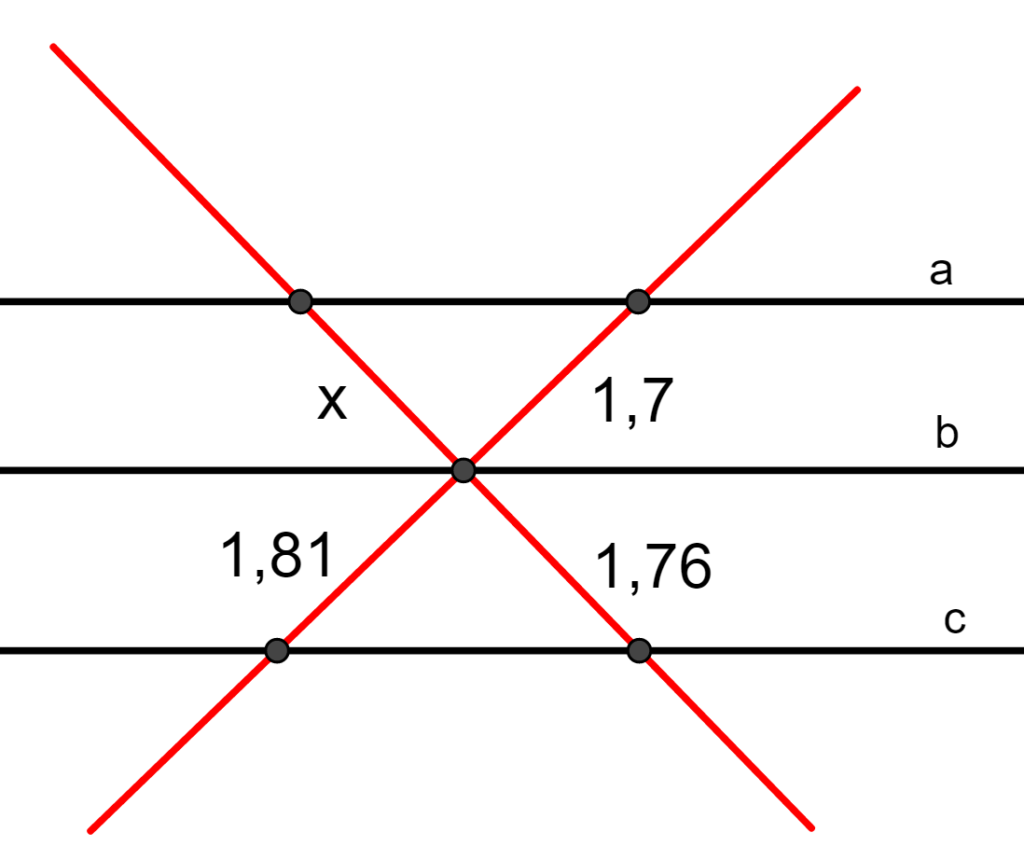
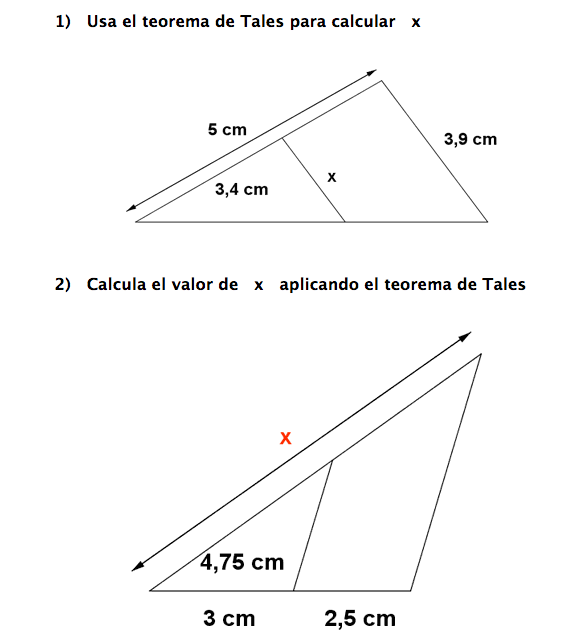
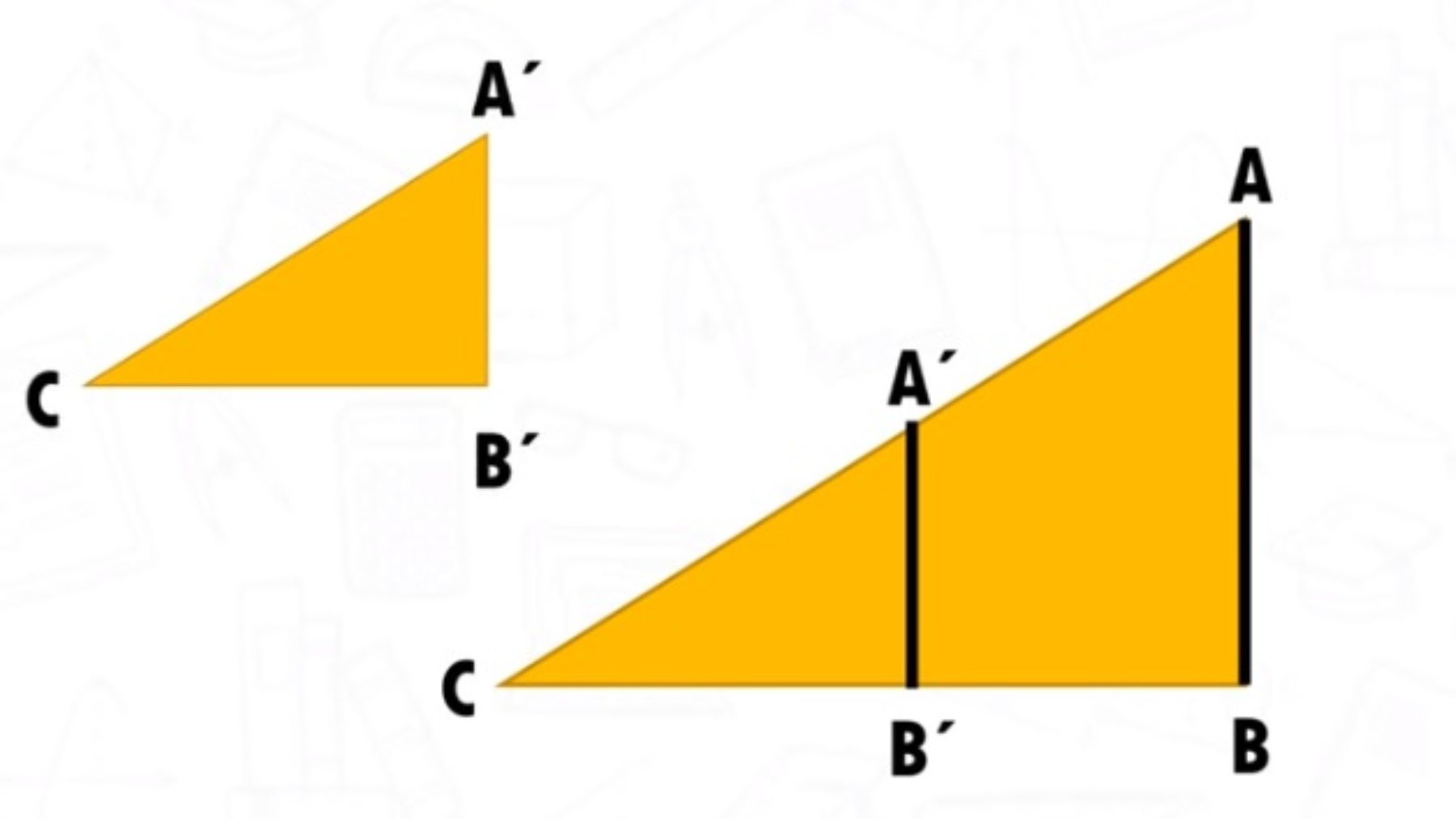
Ele é utilizado para auxiliar no encontro de medidas desconhecidas. O enunciado do teorema de Tales diz o seguinte: Dado um feixe de retas paralelas, há segmentos proporcionais sobre duas ou mais retas transversais. As retas r 1 r 2 e r 3 são paralelas, e as retas t 1 e t 2 são transversais. Então, pelo teorema de Tales, temos que:. 1) Usa el teorema de Tales para calcular x . 2) Calcula el valor de x aplicando el teorema de Tales. 3) Halla x e y aplicando el teorema de Tales. 4) Halla x aplicando el teorema de Tales. 5) Halla x aplicando el teorema de Tales. 6) Sabiendo que AB = 15 cm, BC = 20 cm y A'B' = 12 cm, halla la longitud del segmento B'C'. ¿Qué teorema has.
Exercícios sobre Teorema de Tales Lista de questões resolvidas

teorema de Thales Buscar con Google Infographic, Map, Chart

Teorema De Tales Calculadora

Matemática Ejercicios Teorema de Tales YouTube
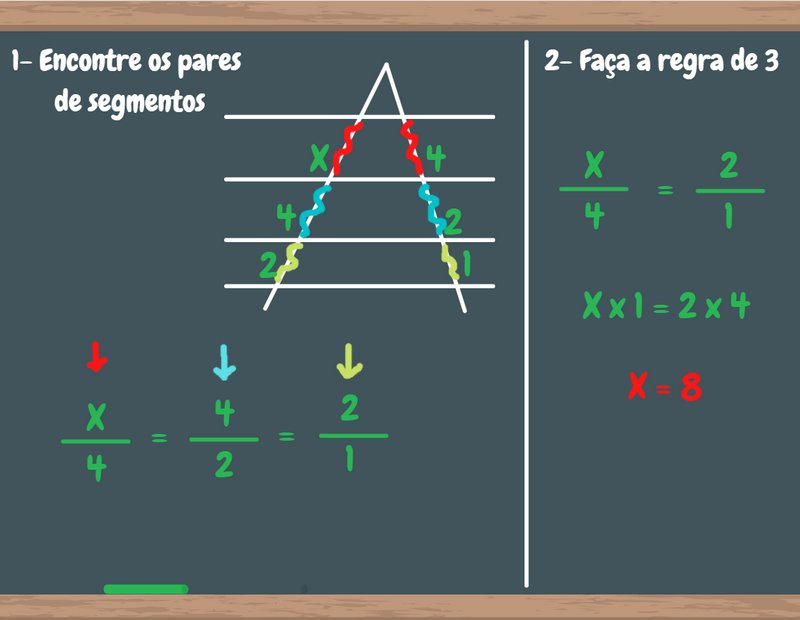
Teorema de Tales exemplos e exercícios resolvidos
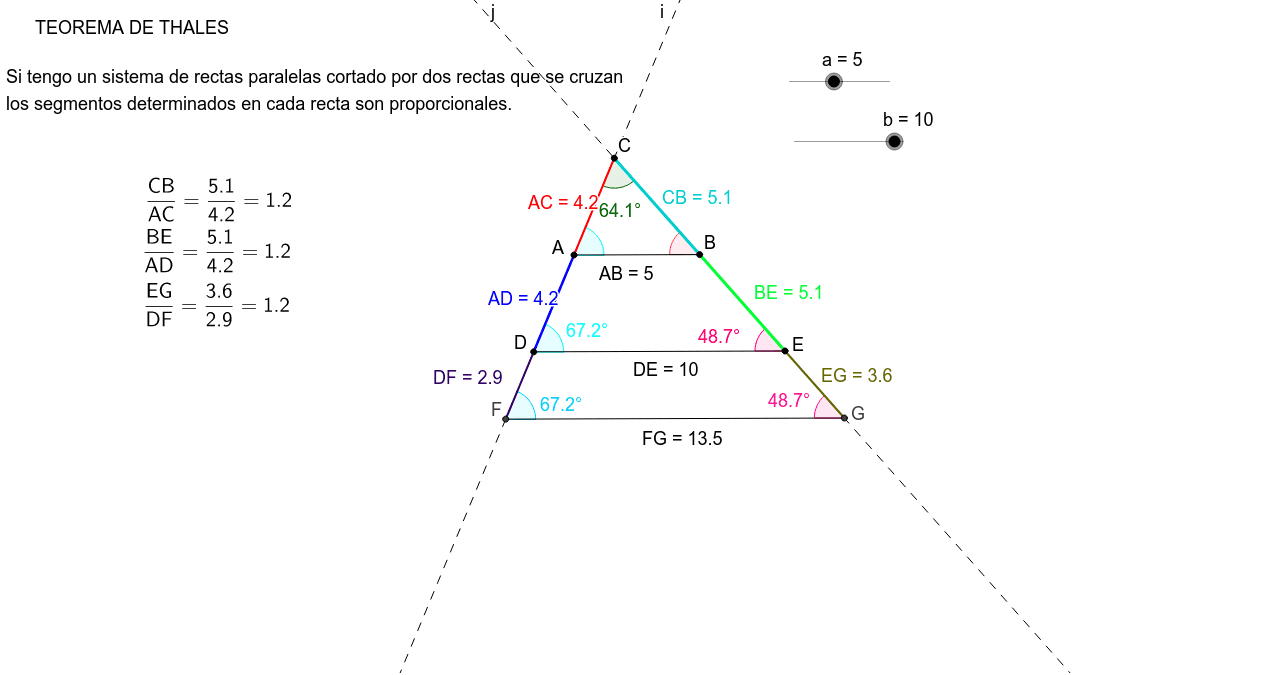
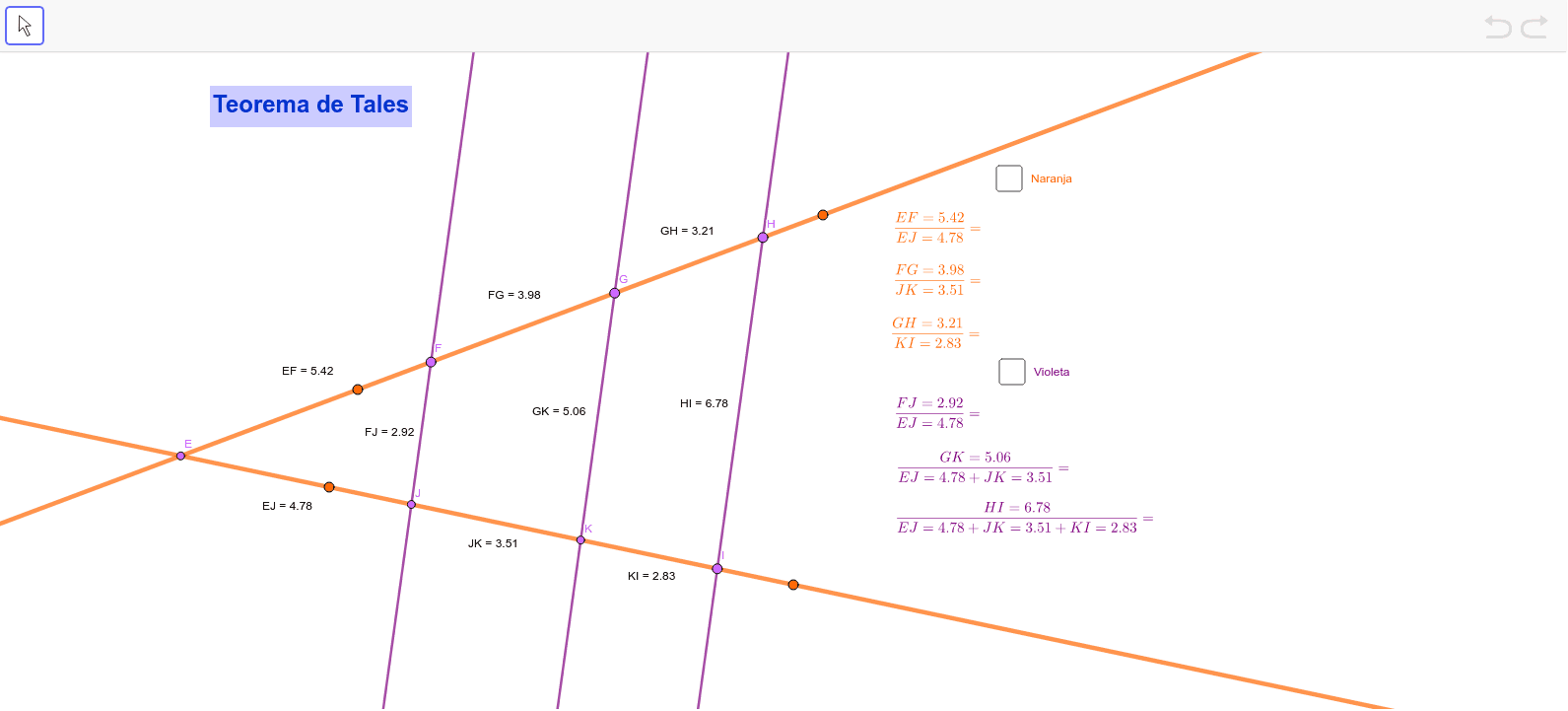
EL TEOREMA DE TALES GeoGebra

Matemáticas contextualizadas con Vilma. Teorema de Tales.

TEOREMA DE TALES Ejercicios. YouTube
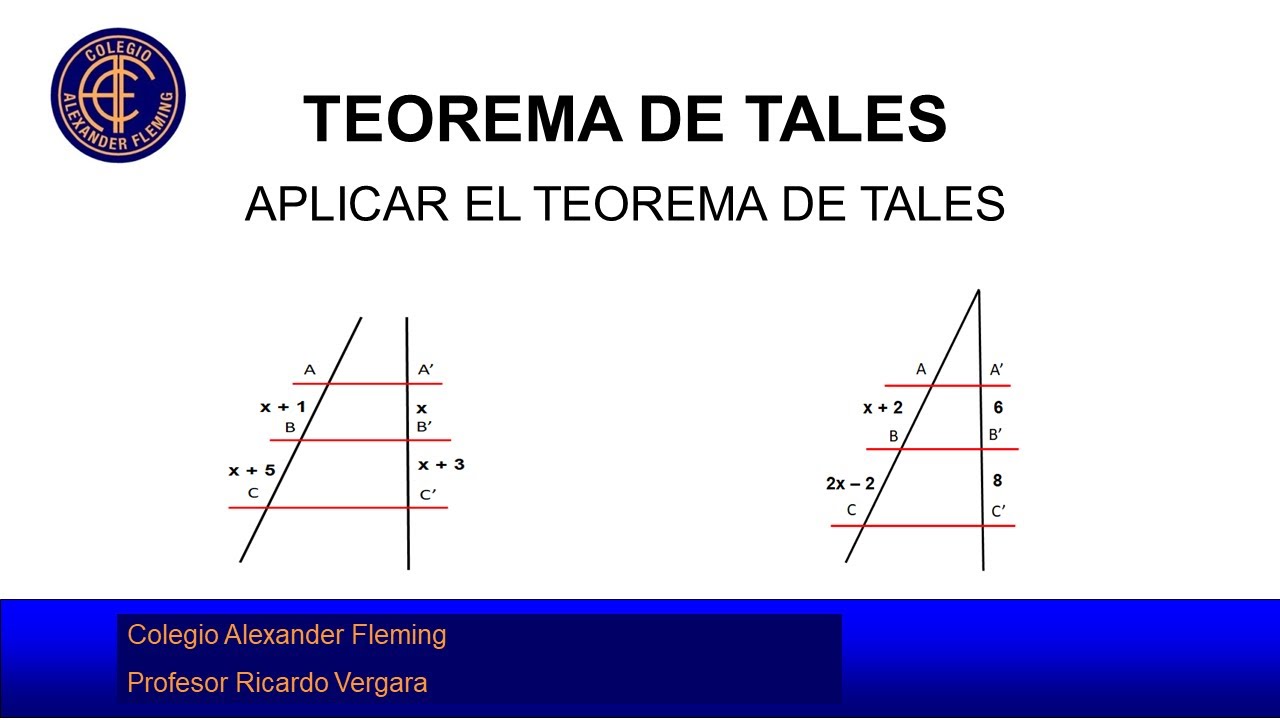
Teorema de Tales YouTube
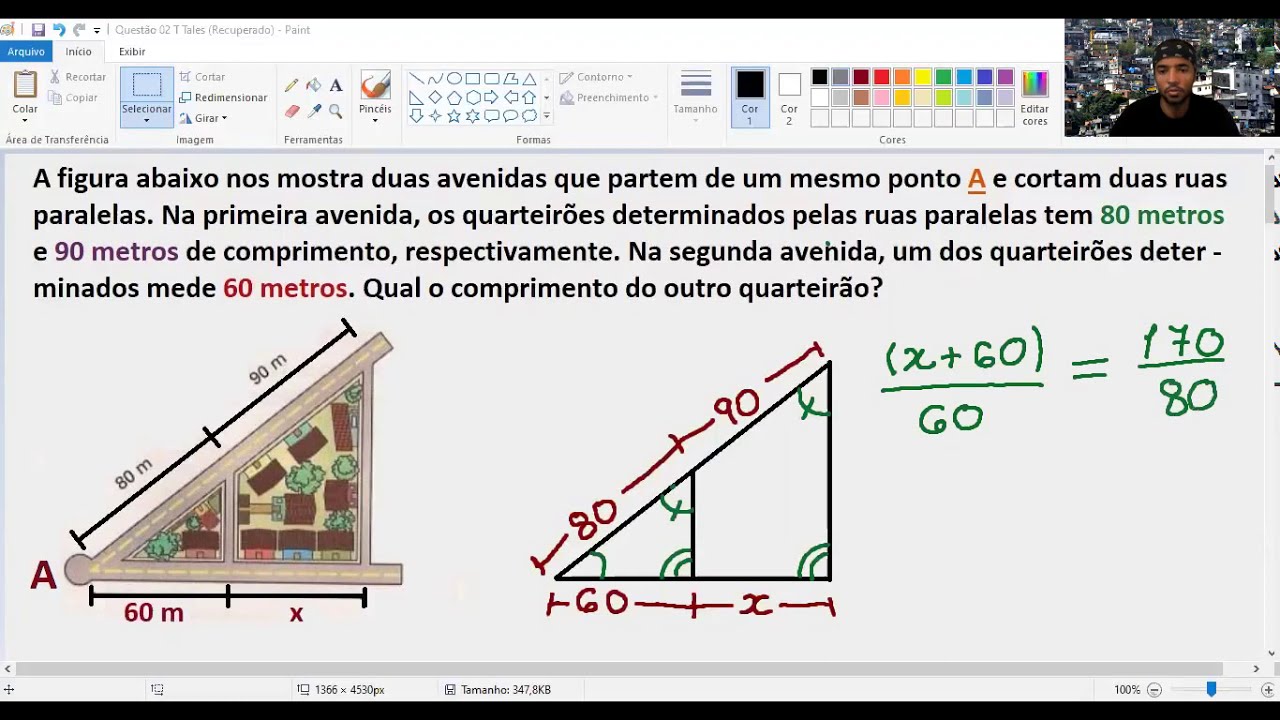
Teorema de Tales exercício resolvido 🌎👣 YouTube
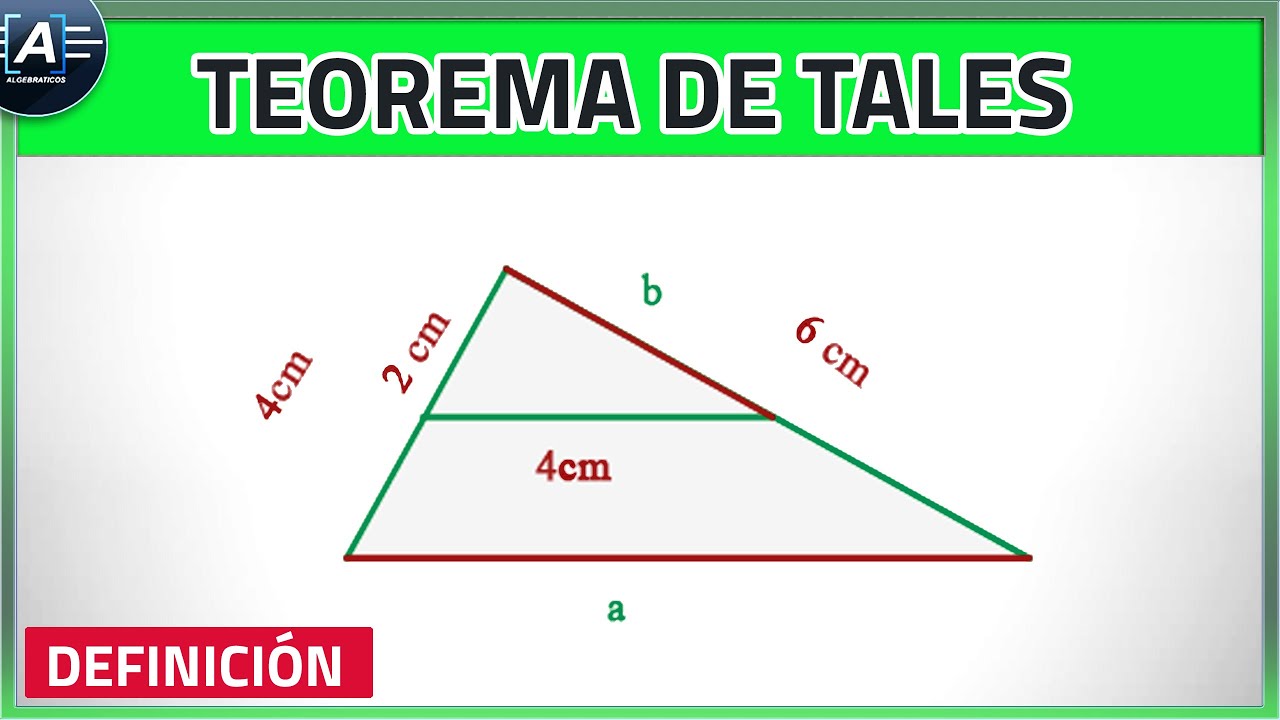
TEOREMA DE TALES Que es el TEOREMA DE TALES (Definición) YouTube
apilar Pase para saber por favor no lo hagas calculadora del teorema de tales Ilegible

Teorema de Tales YouTube
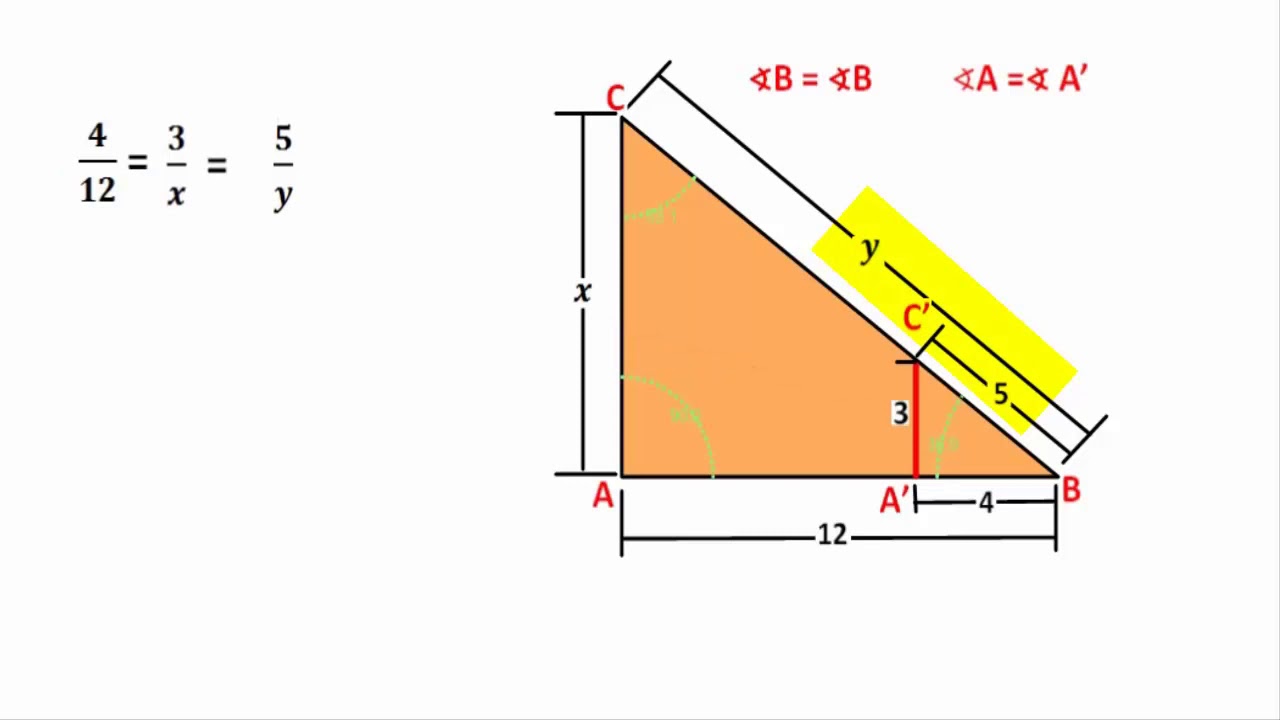
Teorema De Tales Calculadora EDULEARN
Teorema De Tales Calculadora EDULEARN

Teorema De Tales Calculadora Halos

TEOREMA DE TALES. Ejercicio resuelto YouTube
Teorema De Tales Calculadora Halos

Ejercicios de teorema de Tales. Triángulos semejantes YouTube
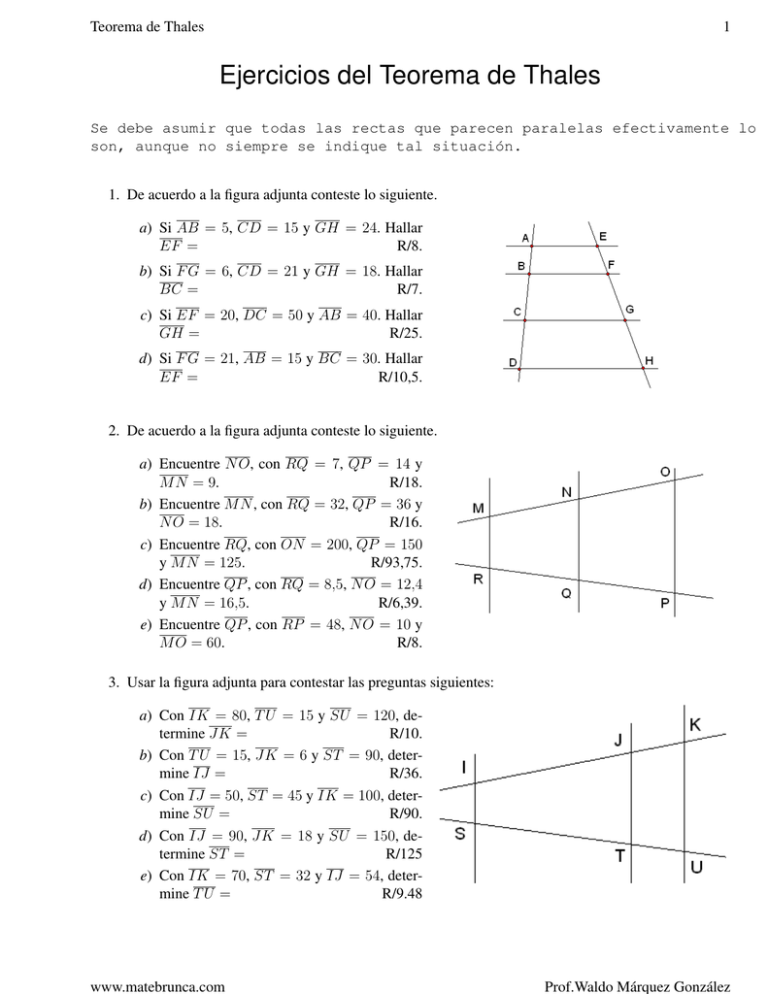
Ejercicios del Teorema de Thales
AN = y AC =. MN = y BC =. La calculadora del Teorema de Tales de Mileto ha sido creada con el objetivo de brindar a nuestros usuarios una herramienta que les ayude a comprender dicho teorema de forma clara y sencilla. Con esta herramienta aprenderás fácilmente a utilizar el teorema de Thales ya que ofrece soluciones detalladas paso a paso.. El teorema de Tales te permite calcular la longitud de un segmento, conocidos los valores de todos los demás segmentos de dos rectas que se encuentran en posición de Tales. Encontrarse en posición de Tales significa que las rectas tienen que estar tal y como dice el teorema de Tales, es decir, dos rectas secantes cortadas por varias rectas.